「数独の解き方」一つの方法
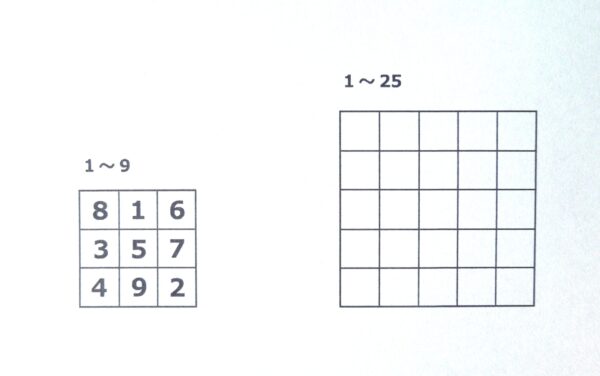
さて、数独の解き方に入る前に、本題と違いますが上の写真を
見てください。魔法陣の例ですが、左の9個のマス目に1~9まで
の数字が入っています。
ご存知の簡単な魔法陣ですが、
出題は、「空欄に1~9の数字を使ってタテ・ヨコ・ナナメの和が同じ
になるように配列しろ」という問題です。(正解は写真のよう
になります。)
この問題は、いろいろと数字を入れてみて割合と簡単に解けました。
右の写真は、25個のマス目に1~25の数字を入れて同様にタテ・
ヨコ・ナナメの和が同じになるようにしなさいという出題です。
下のコツでやってみてください。)
マス目が少なければ良いですが、さらには、7×7、9×9、11×11
、、、というような奇数のマス目に、1~49、1~81、1~121の
数字を入れるようにマス目を増やされると複雑でわけが解らなくなります。
そこで、なにかコツというか法則が有るのではないかと考えました。
有りました。1から順番に一定の順序で入れて行きます。そのやり方でやる
と簡単に配列できるようになり、タテ・ヨコ・ナナメの和も同じになります。
それは次のようなものです。
「コツの手順」
(写真左3×3のマス目の1~9までの数字を追いながらみてください。)
※上段の真ん中に数字1を入れます。
※数字2は、数字1の位置から右斜めに一つ上がり、空欄が無いので一番
下まで下がったマスに入れます。
※数字3は、数字2の位置から右斜に一つ上がり、空欄が無いので一番
下まで下がろうとしますが、ここにも空欄が無いので、一番左まで横に
行った空きマスに入れます。
※数字4は、数字3の位置から右斜に一つ上がろうとしますが、最初に
入れた1が既に埋まっていますから、この場合は、直ぐ下のマスに入
れます。
※数字5は、順当に斜めに進んで入れます。
※数字6は、これも順当に同じように入れます。
※数字7は、右に一つ上がり空欄がなく、一番下にも一番左にも、角
(カド)だから行き場がないのでこの場合は、やはり直ぐ下のマスに
入れます。(行き場がない時は直ぐ下に入れることになります。)
※数字8は、数字3のときと同じように一番左のマスに入れます。
※数字9は、数字2のときと同じように一番下のマスに入れます。
これで完成です。(マス目が増えても同じです。)
(但し、奇数のマス目の場合で、4×4、6×6、8×8の偶数のマス目
では活用できません。)
いよいよ本題の「数独の解き方」です。
数独は簡単なものから超難題まであり、何分でできるか何時間でできる
か何日かかるか、、、。数字の配列は無数で恐らく天文学的な種類になる
のではないかと思われます。
出題は沢山ありますね。
ほとんど毎日、朝日新聞の朝刊(土曜日beを含む)で楽しんでいます。
☆1個の簡単なものから、☆5個の難しいものまでを自分なりのやり方で
数字を入れています。
その方法は、
「ヨコ3段からスタート」
※あらかじめ上段3行・中段3行・下段3行のヨコ3行に幾つかの数字が
入っていて、合わせて9行有りますが、上段3行から始めます。
※上段の左右を見て、2個の数字が決まっているものを探し有れば3個目を
入れます。(2個ないものは保留。)
※中段の左右を見て、2個の数字が決まっているものを探し有れば3個目を
入れます。(2個ないものは保留。)
※下段の左右を見て、2個の数字が決まっているものを探し有れば3個目を
入れます。(2個ないものは保留。)
「次にタテ行に移ります」(左右上下は違いますがやり方は同じです。)
※あらかじめ右列3行・中列3行・左列3行のタテ3行に幾つかの数字が
入っていて、合わせて9行有りますが、右列3行から始めます。
※右行の上下を見て、2個の数字が決まっているものを探し有れば3個目を
入れます。(2個ないものは保留。)
※中行の上下を見て、2個の数字が決まっているものを探し有れば3個目を
入れます。(2個ないものは保留。)
※左行の上下を見て、2個の数字が決まっているものを探し有れば3個目を
入れます。(2個ないものは保留。)
※上段・中段・下段と右列・中列・左列と共通ですが、単独の数字のために、
2個目3個目が入らない場合は、1~9のそれぞれの数字を順番に上下左右
に辿り2つだけ入る空欄が有れば、見込み数字として仮に入れておきます。
(場合により1つの空欄で決まるときもあります。)
※マス目2個に2種類の(ここにしか入らない)決まり数字を見つけます。
(この数字をABとします。)
※これで何個か数字が入りますが、入らない部分のマス目には入る可能性の
ある数字全て(ABを除く)を列記します。
※ヨコ3行を例にしますが、3行の上段・中段・下段で、入る可能性数字
(例えば2)が上段と下段に重なる場合、残りブロックの中段のマス目に
は、決まって2が入ります。(タテ3列も同じ)
※各ブロック(9個のマス目)に、
1.出題された決まり数字
2.2個から追って行き3個目の決まり数字
3.AとBの決まり数字
4.3行の端2列に入る可能性数字が重複する時に中の行に入る決まり数字
5.上記の1.2.3.4以外の見込み数字を入れることにより、全てのマス目
に数字を入れます。(AとBの決まり数字の入る二つのマス目は除きます。)
この手順で、ほとんどの出題は解決できると思います。
以上は、☆1個から☆5個までの「数独」解く場合ですが、次にインターネット
で見つけた数独世界一の超難題を紹介します。

これが難題でした。やり直し書き直しを何10回も試みましたが出来ません。
良いところまで行くのですが、最終段階で入る数字がダブりで入らないのです。
1箇所違うと修正どころか最初からやり直しになります。それでも、繰り返せ
ば何とかなると思い挑戦しましたが駄目でした。
途中で投げ出して、かれこれ2年にもなります。
☆1個や☆5個とはレベルが違います。この出題は何と☆11個。
普通のやり方では出来そうも有りません。
「何回も数字を入れ替え偶然に出来た。」のでは時間も掛かるし面白く無い
し、なるべく短時間で独自の方法で楽しみたいのです。
「何か、法則が有るに違いない」と考えました。
本題に入る前に魔法陣を持ち出したのは、自分で魔法陣の解き方のコツを
考えたささやかな経験があったからです。
数独の解き方の、追加の一つのコツを見つけたのは、つい最近のことです。
それにより、2024年12月8日に「世界一数独」を解決しました。
重い肩の荷がやっと降りました。
笑われるかも知れませんが、この「コツの追加」は次のようなものです。
1~9までの数字の入る9個のマス目を1ブロックとして、タテ・ヨコ3列
で9ブロック中のどれか一つを選んで考えます。
上段の3個のマスに入る数字を足し算して、その和が奇数になるか偶数に
なるかということに、統一性があるのではないかと思ったのです。
※9ブロック全部を調べましたが、一つのブロックの3行について、1行が
奇数なら他の2業は偶数になるか、稀ですが3行共奇数になっていました。
組み合わせによって、ヨコの行・タテの行共3行それぞれが奇数というの
は有ります。
※入れる数字は1から9までですが、奇数が5個・偶数が4個で偶数が1個
少ないから全部が偶数にならない訳です。
※タテ3行・ヨコ3行に3個づつ1~9の数字が入り一つのブロック完成と
なりますが、前後左右の他のブロック内の数字の位置関係で一つのブロッ
クにどの数字が入るかが影響され決まります。
※さらに、他のブロックに既に入っている数字の奇数・偶数によっても入れ
る数字を選択しなければならないようです。これが、重要なヒントになり
ました。
前記の各ブロック(9個のマス目)1~5のコツに追加して試したのですが
選ぶ数字が特定出来て、効率が上がり、やっと正解に辿り着けました。
以上でございます。




最近のコメント